Differential equations – Nonlinear differential equations – Autonomous systems

We consider autonomous systems of the form

\[\frac{dx}{dt}=F(x,y)\quad\text{and}\quad\frac{dy}{dt}=G(x,y),\]

where \(F\) and \(G\) only depend on \(x\) and \(y\) and not explicitly on \(t\).

A point \((x_0,y_0)\) is called a critical point or stationary point of the system if both \(F(x_0,y_0)=0\) and \(G(x_0,y_0)=0\). The system is called locally linear in such a critical point \((x_0,y_0)\) if \(F\) and \(G\) have continuous second-order partial derivatives at \((x_0,y_0)\). In that case are

\[F(x_0,y_0)+F_x(x_0,y_0)(x-x_0)+F_y(x_0,y_0)\]

and

\[G(x_0,y_0)+G_x(x_0,y_0)(x-x_0)+G_y(x_0,y_0)(y-y_0)\]

good approximations of \(F(x,y)\) and \(G(x,y)\) respectively. So then we have:

\[F(x,y)\approx F(x_0,y_0)+F_x(x_0,y_0)(x-x_0)+F_y(x_0,y_0)\]

and

\[G(x,y)\approx G(x_0,y_0)+G_x(x_0,y_0)(x-x_0)+G_y(x_0,y_0)(y-y_0)\]

near the critical point \((x_0,y_0)\). Since \((F(x_0,y_0)=0\) and \(G(x_0,y_0)=0\), then we have:

\[\frac{d}{dt}\begin{pmatrix}x-x_0\\y-y_0\end{pmatrix}\approx\begin{pmatrix}F_x(x_0,y_0) & F_y(x_0,y_0)\\G_x(x_0,y_0) & G_y(x_0,y_0)\end{pmatrix} \begin{pmatrix}x-x_0\\y-y_0\end{pmatrix}.\]

This implies that the behaviour of the solutions near such a critical or stationary point \((x_0,y_0)\) is similar to the behaviour of the solutions of the corresponding linear system (near the origin). The matrix

\[\begin{pmatrix}F_x(x,y) & F_y(x,y)\\G_x(x,y) & G_y(x,y)\end{pmatrix}\]

is called the Jacobi matrix of the system.

Exceptions:

The behaviour of the solutions of the linear system can be obtained from the eigenvalues (and eigenvectors) of the matrix

\[\begin{pmatrix}F_x(x_0,y_0)&F_y(x_0,y_0)\\G_x(x_0,y_0)&G_y(x_0,y_0)\end{pmatrix}.\]

There are two exceptions:

1. \(r_1=r_2=r\in\mathbb{R}\): the origin \(O\) in the linear system is a proper or an improper node. In the nonlinear system the critical or stationary point \((x_0,y_0)\) might also be a spiral point (the stability is determined by the sign of \(r\)).


2. \(r_{1,2}=\pm i\beta\) with \(\beta\in\mathbb{R}\): the origin \(O\) in the linear system is a center point. In the nonlinear system the critical or stationary point \((x_0,y_0)\) might also be a spiral point (with unknown stability).

Examples:

1) \(\displaystyle\frac{dx}{dt}=4-2y\) and \(\displaystyle\frac{dy}{dt}=12-3x^2\). The critical/stationary points are \((\pm2,2)\). The Jacobi matrix is \(J(x,y)=\begin{pmatrix}0&-2\\-6x&0\end{pmatrix}\).

Now we have \(J(-2,2)=\begin{pmatrix}0&-2\\12&0\end{pmatrix}\) with eigenvalues \(\pm2i\sqrt{6}\). Hence: \((-2,2)\) is a center of spiral point with unknown stability.

Further we have that \(J(2,2)=\begin{pmatrix}0&-2\\-12&0\end{pmatrix}\) with eigenvalues \(\pm2\sqrt{6}\). Hence: \((2,2)\) is an unstable saddle point.

In this case we have that \(\displaystyle\frac{dy}{dx}=\frac{12-3x^2}{4-2y}\) is separable with implicit solution \(4y-y^2-12x+x^3=c\), where \(c\) is an arbitrary constant. For some values of \(c\) these solutions are drawn in the following pictures:

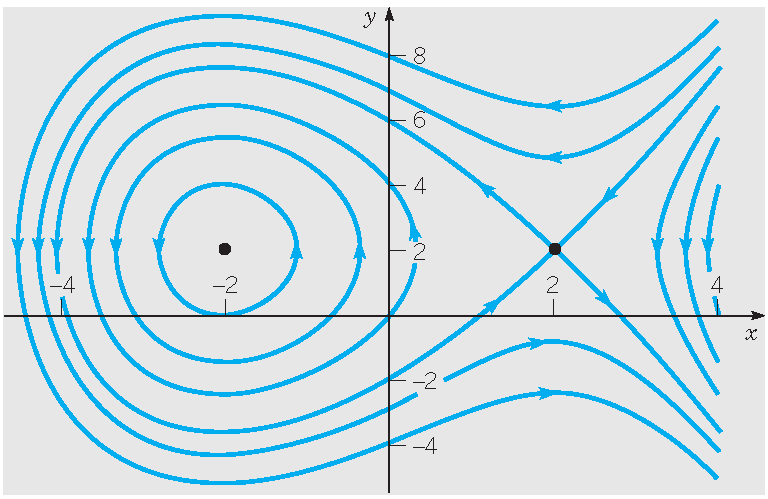
The curve (with \(c=-12\)) starting at the saddle point \((2,2)\), moving to the left and finally returning to \((2,2)\) is called a separatrix.

2) \(\displaystyle\frac{dx}{dt}=-(x-y)(1-x-y)\) and \(\displaystyle\frac{dy}{dt}=x(2+y)\). For the critical/stationary points we have:

\[\left\{\begin{array}{r}-(x-y)(1-x-y)=0\\[2.5mm]x(2+y)=0\end{array}\right.\quad\Longrightarrow\quad(0,0),\;\;(0,1),\;\;(-2,-2),\;\;(3,-2).\]

The Jacobi matrix is \(J(x,y)=\begin{pmatrix}2x-1&1-2y\\2+y&x\end{pmatrix}\).

Hence: \(J(0,0)=\begin{pmatrix}-1&1\\2&0\end{pmatrix}\) with eigenvalues \(-2\) and \(1\). Hence: \((0,0)\) is an unstable saddle point.

Further we have \(J(0,1)=\begin{pmatrix}-1&-1\\3&0\end{pmatrix}\) with eigenvalues \(-\frac{1}{2}\pm\frac{1}{2}i\sqrt{11}\). Hence: \((0,1)\) is an asymptotically stable spiral point.

And \(J(-2,-2)=\begin{pmatrix}-5&5\\0&-2\end{pmatrix}\) with eigenvalues \(-5\) and \(-2\). Hence: \((-2,-2)\) is an asymptotically stable node.

Finally we have \(J(3,-2)=\begin{pmatrix}5&5\\0&3\end{pmatrix}\) with eigenvalues \(3\) and \(5\). Hence: \((3,-2)\) is an unstable node.

3) \(\displaystyle\frac{dx}{dt}=(2-y)(2x-y)\) and \(\displaystyle\frac{dy}{dt}=(2+x)(x-2y)\). For the critical/stationary points we have:

\[\left\{\begin{array}{r}(2-y)(2x-y)=0\\[2.5mm](2+x)(x-2y)=0\end{array}\right.\quad\Longrightarrow\quad(0,0),\;\;(-2,-4),\;\;(-2,2),\;\;(4,2).\]

The Jacobi matrix is \(J(x,y)=\begin{pmatrix}2(2-y)&-2x+2y-2\\2x-2y+2&-2(2+x)\end{pmatrix}\).

Hence: \(J(0,0)=\begin{pmatrix}4&-2\\2&-4\end{pmatrix}\) with eigenvalues \(\pm2\sqrt{3}\). Hence: \((0,0)\) is an unstable saddle point.

Further we have \(J(-2,-4)=\begin{pmatrix}12&-6\\6&0\end{pmatrix}\) with double eigenvalue \(6\). Hence: \((-2,-4)\) is an unstable node or an unstable spiral point.

And \(J(-2,2)=\begin{pmatrix}0&6\\-6&0\end{pmatrix}\) with eigenvalues \(\pm6i\). Hence: \((-2,2)\) is a center or spiral point with unkown stability.

Finally we have \(J(4,2)=\begin{pmatrix}0&-6\\6&-12\end{pmatrix}\) with double eigenvalue \(-6\). Hence: \((4,2)\) is an asymptotically stable node or an asymptotically stable spiral point.

---

Last modified on August 16, 2021